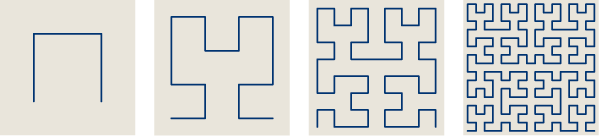
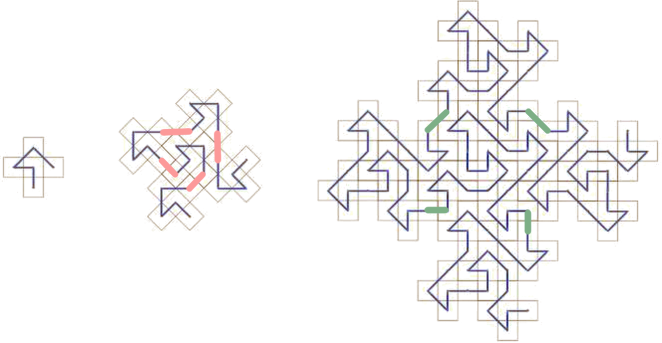
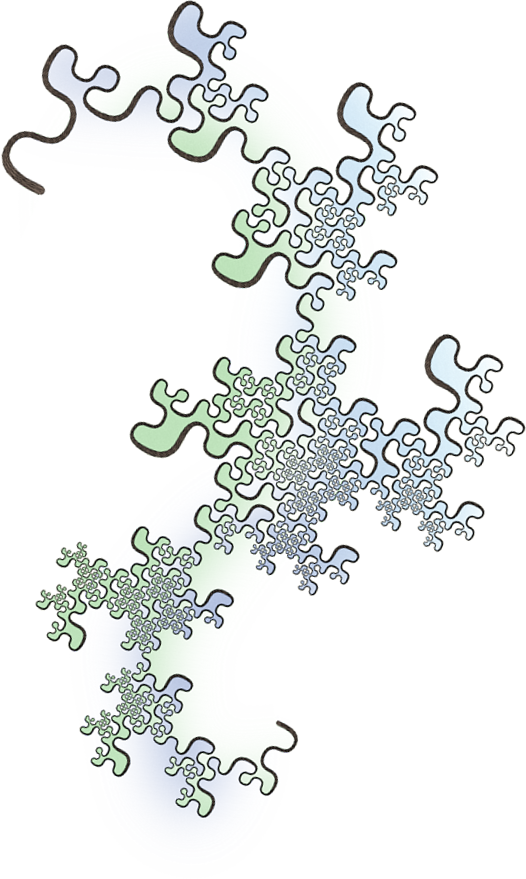
Here’s one of the fractal curves described by Doug McKenna in his new interactive electronic book, Hilbert Curves -Outside-In and Inside-Gone, available on iPad/iPhone.

How would you describe the outline of this shape? That’s a loaded question.
————-
The depth of Doug McKenna’s fractal curviness is not only demonstrated in his latest works; he was developing fundamental designs and curve concepts at the dawn of the Fractal Age.
Of course, Peano, Koch, Sierpinski, and others had already published their now-famous curves long ago. But the craft of making fractal curves truly got its start in the late 60’s, when the Dragon curve was discovered, and then through the 70’s – around the time when Benoit Mandelbrot was working on his thesis on fractals. Some of the people who were hired to design fractal illustrations under Mandelbot’s direction (including Doug) got overshadowed. This is partially due to Mandelbrot’s well-deserved clout, but it is also because of Mandelbrot’s notorious habit of not giving proper attribution to key people on his team.
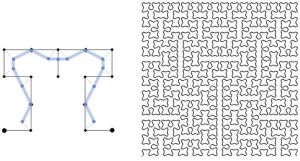
I want to shine some light on one of the earliest inventors of the field. Here’s another picture; this one is from one of Doug’s papers.
As you can see, the motif at left is multiplied many times to fill the interior of the shape to the right of it. It consists of a single self-avoiding curve. The third iteration, shown to the right of that, is also self-avoiding (although the image resolution is too coarse to show this).
There is a certain kind of fuzziness that accumulates on the horizontal edges at each level of iteration, as if ever-smaller forms of moss were growing on the backs of larger forms of moss. Okay; choose your own metaphor, but you get the idea. This is a way of thinking about fractal boundaries – as layers of fuzz.
And fuzz…comes in many forms!
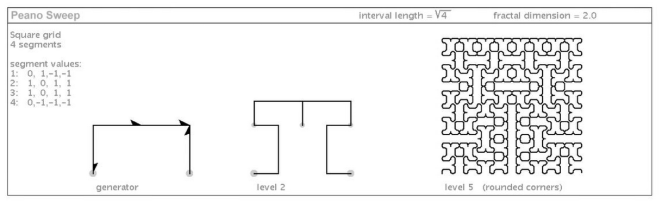
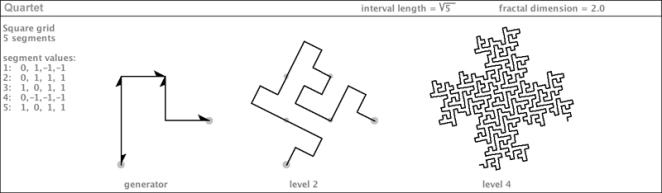
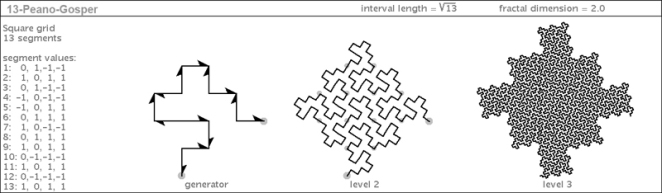
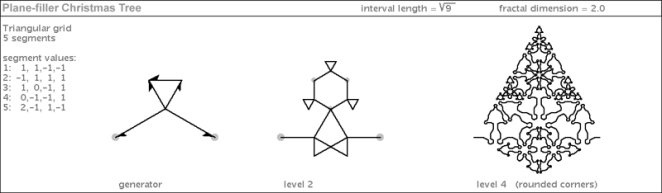
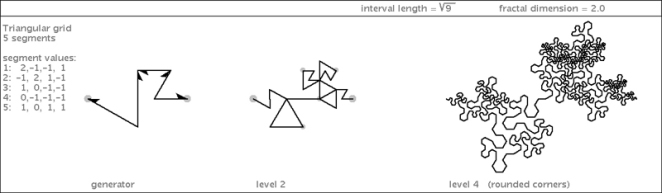
I came across this mind-bending concept while trying to describe the boundaries of some curves I had discovered. My latest book illustrates three plane-filling curves that have different degrees (and kinds) of ruggedness in their boundaries:
The boundary of the first curve is straight (not counting the corners). The more times it is iterated, the more that straightness gets expressed. The fractal dimension of its boundary is 1. In contrast, the second curve has a rather convoluted boundary (with a much higher fractal dimension). Not only does the boundary pinch itself off in accumulating wasp-waist points at every iteration, but parts of its boundary appear to get closer with every iteration, perhaps self-contacting at infinity. This curve is not filling a simple-boundary topological unit in the plane; it is splitting itself into an infinity of body parts and even leaving holes (tremas) as it iterates.
But the topological weirdness gets more weird when you try to describe the boundary of the third curve. This curve, when sufficiently iterated, turns itself into a sort of “plane-filling gasket” (fyi – Gasket fractals are well-studied and illustrated). Forget about trying to identify its interior from its exterior – it’s impossible with this curve.
 Well, seeing Doug’s new curves reminded me of this paradoxical nature of fractal curve boundaries.
Well, seeing Doug’s new curves reminded me of this paradoxical nature of fractal curve boundaries.
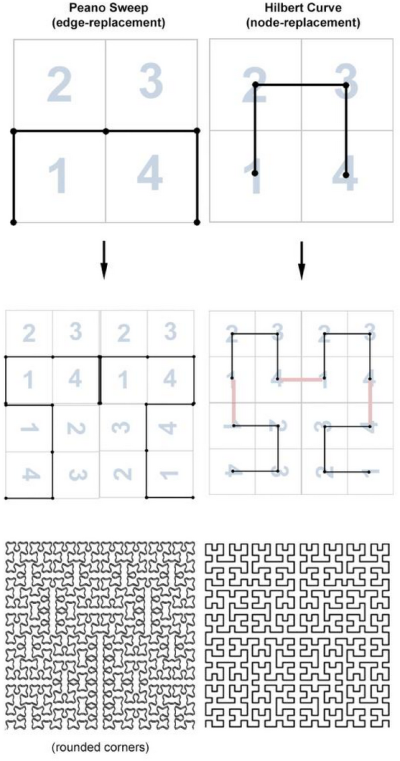
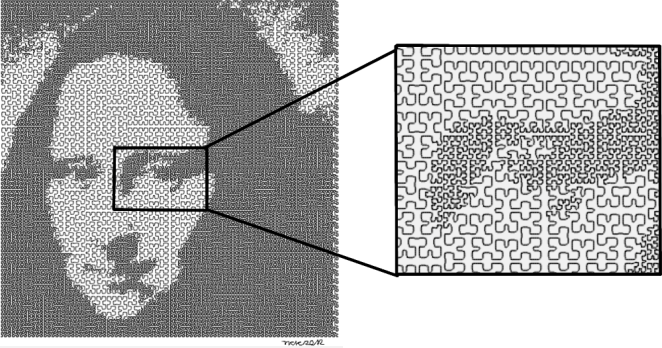
As soon as you start to think of the boundary of a fractal curve as a fractal in itself, things start to get really meta. This is one of the concepts highlighted in Doug’s new book, which, extends the Hilbert curve into an infinite hierarchy of ever-complexifying variations.

In the 1994 conference proceedings, The Lighter Side of Mathematics, there is paper written by Doug, called SquaRecurves, E-Tours, Eddies, and Frenzies: Basic Families of Peano Curves on the Square Grid. This paper introduces some of his earlier explorations. Here is an illustration from that paper:

Doug identified several classes of related curves that are all self-avoiding. I reconstructed some of his curves for my book. Here are a few of those illustrations. 
These boundaries are fairly easy to see. In fact the E-curve, fills a square, like the Hilbert curve. But with so much potential variation, it doesn’t take much genetic manipulation to turn a square-filling curve into a wild and crazy beast.
Wikipedia occasionally lies. Here’s one such lie: “a space-filling curve is a curve whose range contains the entire 2-dimensional unit square.”
Such a lack of imagination…as well as being wrong.
I challenge anyone to tell me that the following space-filling curve is a square.

If that’s a square, then I’m a Klein bottle.
This curve is an example of Doug’s new “half-domino curves“. It can tesselate with a 180-rotated version of itself to create something at least more square-like, for those of you who are uncomfortable with exterior fuzz.

McKenna’s newer curves extend the basic concept of the Hilbert curve, making it just one instance of a larger class of curves.
 Even within the square, there is an infinite variety of plane-filling sweeps. But some of these curves bust out of their square homes and push the fractal dimension of their boundaries to the point of them becoming their own space-filling curves. That’s meta!
Even within the square, there is an infinite variety of plane-filling sweeps. But some of these curves bust out of their square homes and push the fractal dimension of their boundaries to the point of them becoming their own space-filling curves. That’s meta!





































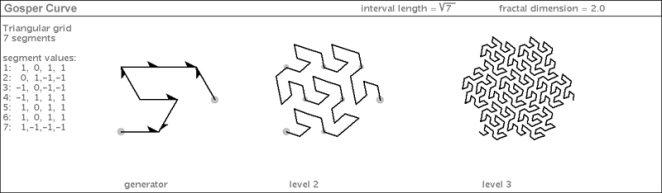


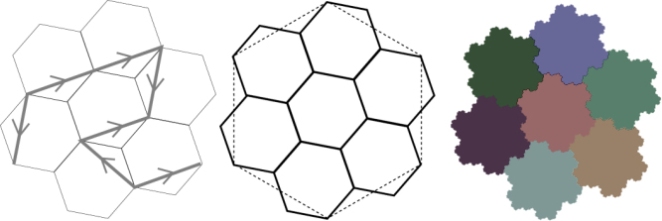

 There are many ways to count a bunch of pennies. In this case you could count them in the order of the Gosper curve’s sweep. Since it is recursive, you could pause every 7 pennies to catch your breath. And you could also pause every 49 pennies for longer breaks. Between each break, you will have traced out a low-order Gosper curve.
There are many ways to count a bunch of pennies. In this case you could count them in the order of the Gosper curve’s sweep. Since it is recursive, you could pause every 7 pennies to catch your breath. And you could also pause every 49 pennies for longer breaks. Between each break, you will have traced out a low-order Gosper curve.




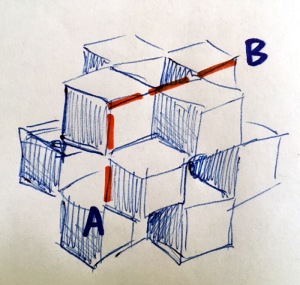 Here’s a picture I drew of 13 unit cubes representing rhombic dodecahedra. (BTW – if you stellate each face of a cube by adding a square pyramid, it becomes a rhombic dodecahedron. And if you start with a “3D checkerboard” of 13 cubes, like I have drawn, the result is 13 tessellating rhombic dodecahedra. Cool, eh? Now, look at red lines in the drawing. the distance from A to B happens to be the square root of 13 (assuming unit cubes).
Here’s a picture I drew of 13 unit cubes representing rhombic dodecahedra. (BTW – if you stellate each face of a cube by adding a square pyramid, it becomes a rhombic dodecahedron. And if you start with a “3D checkerboard” of 13 cubes, like I have drawn, the result is 13 tessellating rhombic dodecahedra. Cool, eh? Now, look at red lines in the drawing. the distance from A to B happens to be the square root of 13 (assuming unit cubes).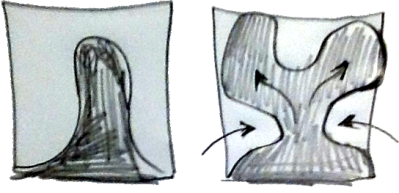 As the dark fluid surges upward, the light-colored fluid around it gets pulled inward, creating a “neck” as shown above at right, and the dark fluid bifurcates at the top. You can compare this shape to the generators for the
As the dark fluid surges upward, the light-colored fluid around it gets pulled inward, creating a “neck” as shown above at right, and the dark fluid bifurcates at the top. You can compare this shape to the generators for the